KAT5-An Experimental Initiative

Buckle up, folks! We’re taking you on a wild ride where two big shots in the tech world team up — the super smart Kolmogorov-Arnold Networks (KANs) and the one-and-only T5 transformer. It’s like when your favorite superheroes join forces, but for the deep learning scene.

In this blog post, we will explore the integration of Kolmogorov-Arnold Networks (KANs) with the T5 transformer model. This experimental initiative aims to leverage the strengths of both architectures to create a more powerful and interpretable deep learning model. We will discuss the working of the merged model, the changes made, benefits, and future scope.

T5

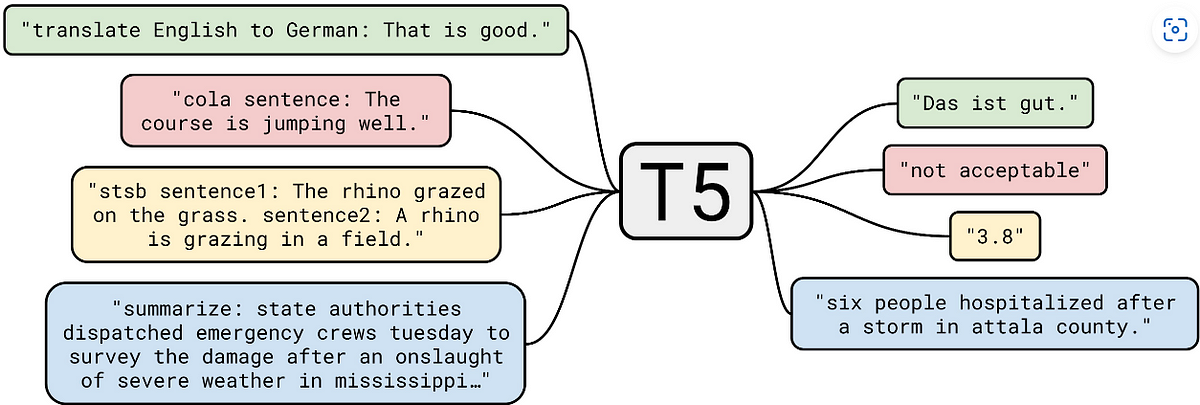
T5, based on the Transformer architecture, revolutionizes NLP by framing all tasks as text-to-text problems. It uses a single model for various tasks, with input prompts guiding output generation. Pretrained on massive text data, T5 can be fine-tuned for translation, summarization, question answering, and more. Its architecture, task-specific heads, and tokenization contribute to its versatility and effectiveness in natural language understanding and generation.

The Kolmogorov-Arnold Network (KAN)

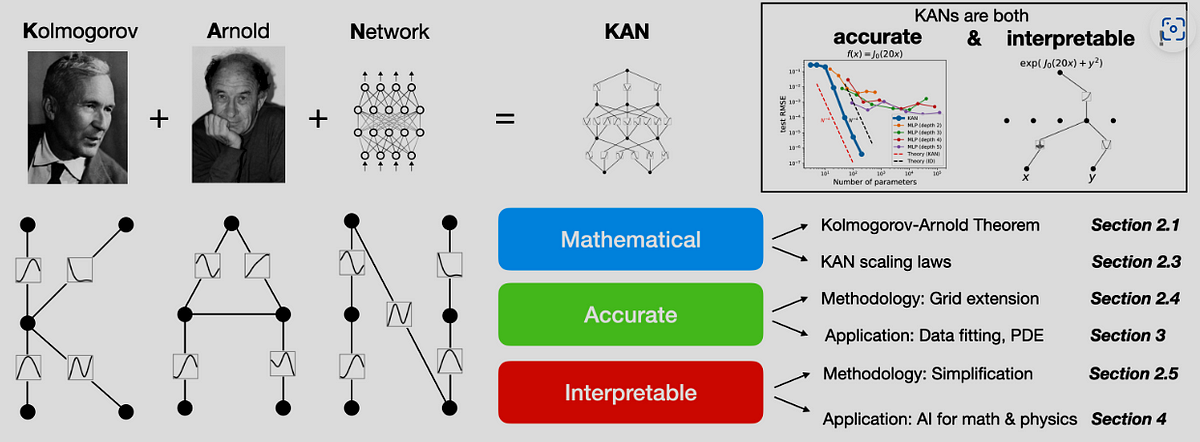
Kolmogorov-Arnold Networks (KANs) are a novel type of neural network architecture inspired by the Kolmogorov-Arnold representation theorem. Unlike traditional Multi-Layer Perceptrons (MLPs), which have fixed activation functions on nodes, KANs introduce learnable activation functions on edges between nodes. These activation functions are represented as splines, replacing the linear weight matrices found in MLPs. The result is improved accuracy, faster neural scaling laws, and enhanced interpretability. KANs offer promising alternatives to MLPs, opening up opportunities for advancing deep learning models.

What motivated me

So, I thought to myself, “What if we get them a personal lyric prompter?” Enter the Key-Value Attention Network (KAN) module, the ultimate memory aid for our forgetful Transformer friends. By slapping on this bad boy, we’re giving T5 the ability to nail those long-range dependencies like a pro, hitting every note perfectly.

An integrated architecture that combines the Transformer model with the Key-Value Attention Network (KAN) module to improve the capability of capturing long-range dependencies in sequences. The reason behind this integration is that while Transformer models like T5 have shown remarkable performance, they can still struggle with modeling long-range interactions effectively. By incorporating the KAN module, which uses spline functions to learn nonlinear mappings, I aimed to enhance T5’s ability to capture long-range dependencies more accurately. This integrated architecture could potentially boost performance on tasks involving long sequences or sequences with intricate long-range patterns, such as document summarization or language modeling.

The complete experimented code

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
from torch.utils.data import DataLoader, TensorDataset

# Positional Encoding
class P_E(nn.Module):
    def __init__(self, model_dimension, expected_max_sequence_length=5000):
        super().__init__()
        pos_en = np.array([
            [pos / np.power(10000, 2 * (i // 2) / model_dimension) for i in range(model_dimension)]
            if pos != 0 else np.zeros(model_dimension)
            for pos in range(expected_max_sequence_length)
        ])
        pos_en[1:, 0::2] = np.sin(pos_en[1:, 0::2])
        pos_en[1:, 1::2] = np.cos(pos_en[1:, 1::2])

        self.pos_en = torch.FloatTensor(pos_en)

    def forward(self, embeddings):
        pe = self.pos_en[:embeddings.shape[1]].to(embeddings.device)
        return embeddings + pe

# Spline Function
class SplineFunction(nn.Module):
    def __init__(self, input_dim, num_knots):
        super(SplineFunction, self).__init__()
        self.num_knots = num_knots
        self.knots = nn.Parameter(torch.randn(num_knots, input_dim))
        self.coefs = nn.Parameter(torch.randn(num_knots, input_dim))

    def forward(self, x):
        batch_size, input_dim = x.size()
        x_expanded = x.unsqueeze(1).expand(-1, self.num_knots, -1)
        knot_weights = torch.max(self.knots - x_expanded, torch.zeros_like(self.knots)).pow(3)
        output = torch.sum(knot_weights * self.coefs, dim=1)
        return output

# KA Network
class KANetwork(nn.Module):
    def __init__(self, input_dim, output_dim, num_knots=10):
        super(KANetwork, self).__init__()
        self.input_dim = input_dim
        self.output_dim = output_dim
        self.num_knots = num_knots

        self.input_splines = nn.ModuleList([SplineFunction(1, num_knots) for _ in range(input_dim)])
        self.output_splines = nn.ModuleList([SplineFunction(1, num_knots) for _ in range(output_dim)])

    def forward(self, x):
        batch_size, seq_len, _ = x.size()
        x = x.view(batch_size * seq_len, self.input_dim)  # Flatten the input tensor

        x = torch.cat([spline(x[:, i:i+1]) for i, spline in enumerate(self.input_splines)], dim=1)
        x = torch.cat([spline(x[:, i:i+1]) for i, spline in enumerate(self.output_splines)], dim=1)

        x = x.view(batch_size, seq_len, self.output_dim)  # Restore the original shape
        return x

# Multi-Head Attention
class mha(nn.Module):
    def __init__(self, h_dim, n_heads):
        super().__init__()
        self.h_dim = h_dim
        self.num_heads = n_heads
        self.norm = nn.LayerNorm(h_dim)
        self.dropout = nn.Dropout(0.2)
        self.softmax = nn.Softmax(dim=2)

    def forward(self, q, k, v, masked):
        rs = q.size()[0]
        q2 = torch.cat(torch.chunk(q, self.num_heads, dim=2), dim=0)
        k2 = torch.cat(torch.chunk(k, self.num_heads, dim=2), dim=0)
        v2 = torch.cat(torch.chunk(v, self.num_heads, dim=2), dim=0)

        outputs = torch.bmm(q2, k2.transpose(2, 1))

        outputs = outputs / (k2.size()[-1] ** 0.5)
        if masked:
            k_masks = torch.sign(torch.abs(k).sum(dim=-1))
            k_masks = k_masks.repeat(self.num_heads, 1)
            k_masks = k_masks.unsqueeze(1).repeat(1, q.size()[1], 1)

            paddings = torch.ones_like(k_masks) * (-2 ** 32 + 1)
            outputs = torch.where(torch.eq(k_masks, 0), paddings, outputs)
            outputs = self.softmax(outputs)
            q_masks = torch.sign(torch.abs(q).sum(dim=-1))
            q_masks = q_masks.repeat(self.num_heads, 1)
            q_masks = q_masks.unsqueeze(-1).repeat(1, 1, k.size()[1])

            outputs = outputs * q_masks
        else:
            outputs = self.softmax(outputs)
        outputs = self.dropout(outputs)

        outputs = torch.bmm(outputs, v2)
        outputs = outputs.split(rs, dim=0)
        outputs = torch.cat(outputs, dim=2)
        outputs = outputs + q
        outputs = self.norm(outputs)

        return outputs

# Encoder-Decoder
class EncoderDecoder(nn.Module):
    def __init__(self, model_dimension, n_heads):
        super().__init__()
        self.mha = mha(model_dimension, n_heads)
        self.ka_network = KANetwork(model_dimension, model_dimension)

    def forward(self, embeddings_wp, enc=None, x_mask=None, y_mask=None):
        multi_head_attention = self.mha(embeddings_wp, embeddings_wp, embeddings_wp, x_mask)
        if enc is not None:
            multi_head_attention = self.mha(multi_head_attention, enc, enc, y_mask)
        ka_output = self.ka_network(multi_head_attention)
        return ka_output

# Transformer
class Transformer(nn.Module):
    def __init__(self, inp_vocab, model_dimension, n_heads, _num_layers):
        super().__init__()

        self._num_layers = _num_layers
        self.emb = torch.nn.Embedding(inp_vocab, model_dimension)
        self.Pos_Embedding = P_E(model_dimension)
        self.dropout = nn.Dropout(p=0.2)
        self.EncoderDecoder = EncoderDecoder(model_dimension, n_heads)

        self._layers = nn.ModuleList()
        for i in range(_num_layers):
            layer = self.EncoderDecoder
            self._layers.append(layer)

        self.linear = nn.Linear(model_dimension, inp_vocab)
        self.log_softmax = nn.LogSoftmax(dim=-1)

    def forward(self, x, y, x_mask, y_mask):
        embeddings = self.emb(x)
        pos_embeddings = self.Pos_Embedding(embeddings)
        embeddings_wp = self.dropout(embeddings + pos_embeddings)
        enc = None
        for layer in self._layers:
            enc = layer.forward(embeddings_wp, enc, x_mask, y_mask)

        embeddings2 = self.emb(y)
        pos_embeddings2 = self.Pos_Embedding(embeddings2)
        embeddings_wp2 = self.dropout(embeddings2 + pos_embeddings2)
        for layer in self._layers:
            dec = layer.forward(embeddings_wp2, enc, x_mask, y_mask)

        lin = self.linear(dec)
        soft = self.log_softmax(lin)
        return soft

# Define a simple dataset and dataloader
X_train = torch.randint(1, 21, (100, 20))
Y_train = torch.randint(1, 21, (100, 20))
dataset = TensorDataset(X_train, Y_train)
dataloader = DataLoader(dataset, batch_size=10, shuffle=True)

# Initialize model, criterion, and optimizer
model = Transformer(inp_vocab=21, model_dimension=128, n_heads=8, _num_layers=2)
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.0001)

# Training loop with gradient checks
for epoch in range(5):
    total_loss = 0
    for X_batch, Y_batch in dataloader:
        optimizer.zero_grad()
        output = model(X_batch, Y_batch, x_mask=None, y_mask=None)
        loss = criterion(output.view(-1, 21), Y_batch.view(-1))
        loss.backward()
        nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0)
        optimizer.step()
        total_loss += loss.item()

        # Check gradients
        for name, param in model.named_parameters():
            if param.grad is not None:
              pass
                # print(f"{name}: mean={param.grad.mean()}, max={param.grad.max()}, min={param.grad.min()}")

    print(f'Epoch {epoch + 1}, Loss: {total_loss / len(dataloader)}')

What changed

Specifically, the key modification lies in the Encoder-Decoder module, where the traditional feed-forward network has been replaced with the KA network. Instead of relying solely on dense layers, the KA network employs a series of spline functions, which are piecewise polynomial functions, to model the input-output mapping more flexibly.

By combining the strengths of the Transformer’s self-attention mechanism with the KA network’s powerful function approximation capabilities, this implementation offers a promising avenue for handling intricate sequence-to-sequence tasks with greater accuracy and expressivity.

In the standard Transformer, the output of the multi-head attention mechanism is typically passed through a feed-forward network, which can be represented as

Where x is the input, W1, W2, b1, and b2 are learnable parameters, and σ is an activation function.

The feed-forward network is replaced by the KA network, which models the input-output relationship using a sum of spline functions. The output of the KA network can be expressed as:

 

• • N: The number of spline functions (knots). Each spline function contributes to the overall output.

• • d: The input dimension. If your input data has multiple features (e.g., pixel values in an image), d represents the number of features.

• • c_i: These are learnable coefficients associated with each spline function. They determine the contribution of each spline to the final output.

• • t_ij: These are learnable knot positions for the i-th spline function and j-th input dimension. Knots define the points where the spline transitions from one behavior to another.

The overall expression represents a combination of spline functions, each influenced by its coefficients and knot positions.

The KA network’s output is a weighted sum of piecewise cubic polynomial functions, where each spline function is defined over a different region of the input space. This non-parametric formulation allows for more flexible and expressive function approximation compared to the traditional feed-forward networks.

With the KA network, the internal representations are now influenced by the non-linear spline functions, potentially capturing more intricate patterns and dependencies within the input sequences.

Mathematically, the output of the modified Transformer can be expressed as:

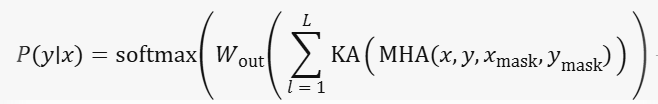
Where L is the number of Encoder-Decoder layers, MHA is the multi-head attention mechanism, KA is the Kolmogorov-Arnold network, W_out and b_out are the learnable parameters of the final output layer, and softmax is the softmax activation function.

How it benefited

 

1. 1. Non-linear Modeling Capability:

 

• • The standard Transformer architecture relies on linear transformations (e.g., linear layers, attention mechanisms) to model the relationships between input and output sequences.

• • The KA network, on the other hand, introduces non-linear spline functions, which can better capture complex, non-linear relationships between the input and output sequences.

• • This non-linear modeling capability is particularly beneficial for tasks involving data with intricate, non-linear dependencies, such as time-series forecasting, speech recognition, or natural language processing tasks with intricate linguistic patterns.

2. Increased Representational Capacity:

 

• • The KA network is a non-parametric method, meaning it can approximate any continuous function on a compact set without being constrained by a fixed number of parameters.

• • By combining the KA network with the Transformer architecture, the resulting model gains a higher representational capacity, allowing it to model more complex and diverse patterns in the data.

• • This increased representational capacity can be particularly advantageous for tasks involving high-dimensional or highly structured data, where the standard Transformer may struggle to capture all the relevant information.

3. Automatic Feature Learning:

 

• • The KA network utilizes spline functions, which have the remarkable ability to automatically learn meaningful representations directly from the input data.

• • This novel approach eliminates the laborious and frequently suboptimal process of manual feature engineering.

• • By automatically learning the most relevant features, the KA network can potentially uncover important patterns and relationships that may be overlooked when relying on manually engineered features, especially in complex data domains.

4. Theoretical Guarantees:

 

• • The KA network is based on the Kolmogorov-Arnold representation theorem, which states that any continuous function on a compact set can be represented as a superposition of sums and products of simpler functions.

• • This theoretical foundation provides guarantees about the approximation capabilities of the KA network, ensuring that it can model any continuous function within the given input domain, given sufficient network capacity.

• • These theoretical guarantees can provide insights into the model’s behavior and potential limitations, facilitating better model design and analysis.

5. Potential Improved Generalization:

 

• • Due to its non-linear modeling capabilities, increased representational capacity, and automatic feature learning properties, the T5 variant with the KA network may generalize better to unseen data, especially in tasks involving complex non-linear relationships.

• • This improved generalization can lead to better performance on real-world tasks, where the data distribution may differ from the training data distribution.

Challenges

 

• • The KA network introduces additional parameters (knots and coefficients for the spline functions), increasing the overall model size and computational requirements.

• • The computational cost of evaluating spline functions can be higher than linear transformations, potentially slowing down training and inference times.

• • Careful optimization and hardware acceleration techniques may be necessary to mitigate the increased computational demands of the KA network.

Limitations

 

1. 1. Fixed Number of Knots: The KAN module uses a fixed number of spline functions (knots) to model the input and output sequences. This may not be optimal for all tasks, as the ideal number of knots could vary depending on the complexity of the problem.

1. 1. Lack of Adaptivity: The KAN module learns a fixed nonlinear mapping between inputs and outputs using spline functions. It may be better to have an adaptive mechanism that can adjust the complexity of the mapping based on the input data or task.

1. 1. Scalability: The computational cost of the KAN module increases as the number of knots and the input/output dimensions grow larger. This could make it challenging to scale the model to very high-dimensional or large-scale problems.

1. 1. Integration with Pre-trained Models: Incorporating the KAN module into pre-trained models like T5 can be complex and may require careful architectural modifications and tuning of hyperparameters.

Future work

 

1. 1. Adaptive Number of Knots: Investigate methods to dynamically determine the optimal number of knots based on the input data or task complexity, rather than using a fixed number.

1. 1. Attention-based Knot Selection: Instead of using a fixed set of knots, explore ways to learn or select knots based on the input data or attention patterns, potentially leading to more adaptive and efficient representations.

1. 1. Sparse KAN: Develop sparse variants of the KAN module, where only a subset of knots or spline functions are active at a given time, reducing computational complexity and enabling scalability to higher-dimensional problems.

1. 1. Integration with Other Architectures: Explore integrating the KAN module with other popular architectures, such as BERT, GPT, or Vision Transformers, to capture long-range dependencies in different modalities or tasks.

1. 1. Theoretical Analysis: Conduct a more in-depth theoretical analysis of the KAN module’s properties, such as its expressiveness, convergence behavior, and the conditions under which it can effectively capture long-range dependencies.

1. 1. Interpretability: Investigate methods to improve the interpretability of the KAN module, potentially by visualizing the learned spline functions or analyzing the attention patterns within the module.

Next time around, we’ll dive deep into crunching the numbers on our variant. We’ll see how it stacks up against the other overachievers out there!

References

KAN: Kolmogorov–Arnold Networks (arxiv.org)

T5 Explained | Papers With Code